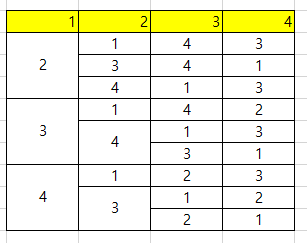
교란순열이란 교란순열(derangement)은 원래 위치에 있지 않은 원소만으로 구성된 순열을 말합니다. 예를 들어, 4개의 원소가 있는 경우 교란순열의 수는 9개입니다. 이를 수학적으로 표현하면, ( D_4 = 9 )입니다. 일반적으로 교란순열의 수를 나타내는 기호는 ( D_n )이며, 간단한 예로 ( D_1 = 0 ), ( D_2 = 1 ), ( D_3 = 2 ) 등으로 계산할 수 있습니다. 교란순열은 조합론에서 중요한 개념으로, 모든 원소가 원래의 위치에 있지 않도록 배열하는 경우의 수를 구하는 문제입니다. 이러한 문제는 ‘모자 문제’ 또는 '모자 확인 문제’라고도 불리며, 고전적인 확률 문제로도 잘 알려져 있습니다. 교란순열의 수를 구하는 방법에는 여러 가지가 있는데, 대표적인 방법으로는 점화식을..