교란순열이란
교란순열(derangement)은 원래 위치에 있지 않은 원소만으로 구성된 순열을 말합니다.
예를 들어, 4개의 원소가 있는 경우 교란순열의 수는 9개입니다.
이를 수학적으로 표현하면, ( D_4 = 9 )입니다.
일반적으로 교란순열의 수를 나타내는 기호는 ( D_n )이며, 간단한 예로 ( D_1 = 0 ), ( D_2 = 1 ), ( D_3 = 2 ) 등으로 계산할 수 있습니다.
교란순열은 조합론에서 중요한 개념으로, 모든 원소가 원래의 위치에 있지 않도록 배열하는 경우의 수를 구하는 문제입니다. 이러한 문제는 ‘모자 문제’ 또는 '모자 확인 문제’라고도 불리며, 고전적인 확률 문제로도 잘 알려져 있습니다.
교란순열의 수를 구하는 방법에는 여러 가지가 있는데, 대표적인 방법으로는 점화식을 이용하는 방법과 포함 배제의 원리를 이용하는 방법이 있습니다. 점화식을 이용하면, $$( D_n = (n-1) \times (D_{n-1} + D_{n-2}) )$$로 표현할 수 있으며, 포함 배제의 원리를 이용하면 $$( D_n = n! \times \left[1 - \frac{1}{1!} + \frac{1}{2!} - \frac{1}{3!} + \cdots + (-1)^n \times \frac{1}{n!}\right] ) $$로 나타낼 수 있습니다.
이러한 교란순열의 개념과 계산 방법은 확률과 통계, 경우의 수를 다루는 수학 문제에서 매우 유용하게 사용됩니다.
교란순열 점화식 원리
n명의 친구가 각각 자기 모자를 테이블에 벗어 놓고 자기 모자가 아닌 모자를 쓰는 경우를 생각해 보자.
1명이라면 0 가지이다.
2명이라면 1번과 2번이 서로 바꿔 쓰는 경우 1가지 이다.
3명이라면 1번은 2,3번 모자를 쓰는 경우 2가지이고 2번은 1번이 쓰고 남은 2개 중 하나를 골라 쓸 수 있다.(1번이 3을 골랐다면 1을,1번이 2를 골랐다면 1 또는 3을 선택할 수 있다) 3번은 2번이 쓰고 남은 것을 고른다. 이때 1번이 2를 2번이 1을 골랐다면 자신은 3을 쓰는데 이것은 불가능 하므로 결국 2가지 이다.
4명인 경우는 아래 그림과 같이 표현 할 수 있을 것이다.
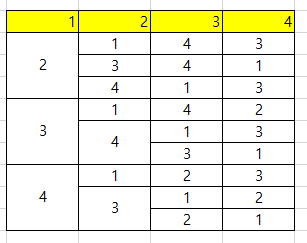
이 것을 점화식으로 살펴 보자.
n개의 원소가 있다면
첫번째 원소는 n-1개의 다른 위치로 갈 수 있다.
이제 두가지 경우를 생각해 볼 수 있다.
1. 첫 번째 원소가 간 위치의 원소가 첫 번째 위치로 온다면 나머지 (n-2)개의 원소는 다시 교란 순열을 이룰 수 있다. 이 경우의 수는 Dn-2 이다.
2. 첫 번째 원소가 간 위치의 원소가 첫 번째 위치로 오지 않는다면 나머지 (n-1)개의 원소 중 하나가 첫번째 위치로 와야 한다. 이 경우 나머지 (n-1)개의 원소는 (n-1) 개의 교란 순열을 이루어야 하므로 이 경우의 수는 Dn-1 이다.
이 두 경우를 합치면 다음과 같은 점화식이 된다.
$$( D_n = (n-1) \times (D_{n-1} + D_{n-2}) )$$
교란순열 포함배제의 원리
교란순열의 포함배제의 원리의 식은 조합론에서 중요한 포함 배제의 원리를 사용한다.
이 과정을 단계별로 살펴 보면 다음과 같다.
1. 순열과 고정점 : n 개의 원소로 이루어진 순열에서 각 원소가 자신의 초기 위치에 있는 경우를 고정점이라고 한다. 교란 순열은 고정점이 없는 순열을 말한다.
2. 고정점의 집합 : Ai 를 i 가 고정점인 순열들의 집합이라고 한다. 그러면 (A1,A2,...An) 은 1,2,...n 이 고정점인 순열들의 집합이다.
3. 집합의 크기 계산 : Ai의 크기는 (n-1)! 이다. 왜냐하면 i를 제외한 나머지 n-1 개의 원소를 재배열 하는 방법의 수와 같기 때문이다.
4. 교집합의 크기 계산 : Ai와 Aj의 교집합 즉 i와 j 가 모두 고정점인 순열의 수는 (n-2)! 이다. 이는 i 와 j를 제외한 나머지 원소들을 재배열하는 방법의 수와 같다.
5. 포함 배제의 원리 적용 : 이제 포함배제의 원리를 적용하여 고정점을 하나도 갖지 않는 순열, 즉 교란순열의 수를 계산한다. 이를 위해 모든 고정점을 갖는 순열들의 집합을 제외한다.
6 교란순열의 수식 도출
$$[ D(n) = n! - \binom{n}{1}(n-1)! + \binom{n}{2}(n-2)! - \binom{n}{3}(n-3)! + \cdots + (-1)^n \binom{n}{n}(n-n)! ] $$
이 식은 n!에서 각각의 고정점을 갖는 순열의 수를 빼고, 두개의 고정점을 갖는 순열의 수를 더하고,세개의 고정점을 갖는 순열을 수를 빼는 식으로 계속된다.
7. 단순화 : 이 식을 단순화 하면 다음과 같은 공식이 나온다.
$$[ D(n) = n! \left(1 - \frac{1}{1!} + \frac{1}{2!} - \frac{1}{3!} + \cdots + (-1)^n \frac{1}{n!}\right) ]$$
이 공식은 n 개의 원소를 가진 순열에서 아무도 자신의 원래 위치에 있지 않을 확률, 즉 모든 원소가 잘못된 위치에 있는 순열의 수를 나타낸다.
'강의자료 > 이산수학문제풀이' 카테고리의 다른 글
| [사고력수학]수열에서 2의 배수와 3의 배수를 제거하기 (11) | 2024.02.07 |
|---|---|
| [검단코딩-정보올림피아드2023초등부]3. 거짓말(5점) (8) | 2024.02.02 |
| [검단코딩-정보올림피아드2023초등부]2.양팔저울(5점) (17) | 2024.01.31 |
| [검단코딩-사고력 수학] 짧은 길의 경로 찾기 (17) | 2024.01.30 |
| [검단코딩-정보올림피아드2023초등부]1. 자율주행(5점) (13) | 2024.01.29 |