원당컴퓨터학원

제가 몇주 전부터 알고리즘 상으로는 최대 600만번 계산이 되어 시간초과가 나올 수가 없는데 (알고리즘상 1초당 최대 1억번 연산 처리를 기준으로 함) 계속해서 타임아웃이 발생하더라구요. 무엇이 문제인지 몰라서 알고리즘은 맞는데 구현이 잘못 된 줄 알고 수십번도 더 제출해 보았는데요...결국 몇주동안 풀지 못했던 문제가...scanf,printf 를 사용하지 않고 cin cout 을 사용해서 타임아웃이 걸렸다는 것을 아는 순간 맥이 쫙 빠지네요...ㅠ.ㅠ 알고리즘으로는 전혀 문제가 없는데 또 다른 알고리즘을 요구하는 문제인줄 알고 알고리즘 해법을 찾으러 구글링 하다가 도저히 해법을 못찾아 포기했던 문제였는데요.. 우연한 계기로 cin cout 이 scanf printf 보다 컴파일 속도가 느린것을 확인했..

유클리드 호제법은 2개의 자연수 또는 정수의 최대 공약수를 구하는 알고리즘의 하나 입니다.정보올림피아드에서 2개의 최대 공약수를 구하는 문제가 종종 나오는데...이때 유클리드 호제법을 이용해서 문제를 풀어 나가면 훨씬 빠르고 유용하게 사용할 수 있습니다.예를 들면 131 과 109 의 최대 공약수를 구하는 문제같은 경우 131이 3의 배수인지 아닌지 판단 하고 109가 3의 배수인지 아닌지 판단 하는 것보다는 다음과 같이 구하면 훨씬 수월하게 풀릴것 같네요.131 % 109 = 22 이므로22 와 109 의 최대공약수와 동일 하고...109 % 22 = 21 따라서 22와 21의 최대 공약수와 동일 하기 때문에 최대공약수는 1이 나오게 됩니다.131이 소수인지 아닌지 판단 하는 것보다 이렇게 판단하는 것..

문제풀이) g(0)=1,g(1)=1,g(2)=2를 반환한다고 되어 있는데...여기서 g의 함수가 무엇을 하는지 먼저 살펴볼 필요가 있을것 같습니다.g(11)이 들어 간다고 하면 i,j,k 가 0 부터 11까지 3중 반복이 됩니다.그런데 어떤 경우에 f(i,j,k) 를 호출해서 r에 누적을 해서 누적한 값을 리턴하게 됩니다.어떤 경우냐 하면 i + 2*j + 3*k == 11 인 경우에 해당합니다.그렇다는 얘기는 다음과 같은 경우에 f(i,j,k)를 호출한다고 볼수 있겠네요.i,j,k 는 다음과 같은 경우 호출 될것 같습니다.i j k 11 0 0 9 1 0 7 2 0 5 3 0 3 4 0 1 5 0 8 0 1 6 1 1 4 2 1 2 3 1 0 4 1 5 0 2 3 1 2 1 3 2 2 0 3 0 1 3..

저희가 아이들과 공부를 하다 보면 별을 찍는 규칙을 많이 어려워 하더라구요. 별을 찍는 형태는 다음과 같은 형태가 나타납니다. -*****--***---* 이런 경우 프로그램은 다음과 같이 반복문을 구성해 주어야 합니다. 먼저 행이 3행이므로 한행 한행 진행하기 위해서는 3번 반복을 해 주어야 합니다. 다음과 같이1행2행3행이렇게 반복을 해야 되므로 for(int i=1;i

오늘은 2018년 정보올림피아드 지역대회 초등부 33번 문제를 풀어 보겠습니다. 이번 문제는 while 문과 do while 문의 사용법과 후치증가 후치감소 등의 연산 작업 하는 내용을 확인하는 아주 간단한 내용입니다. 먼저 a=2, b=2 로 초기화 되어 시작 됩니다. while(b) 문장은 b가 0 이 되면 빠져 나갑니다.b가 0 이 되기 전에a=3, b=1a=4, b=0 이 되어 a=4 에서 while 문을 빠져 나가고..그 다음 do while 문에서는 a가 0 이 되면 빠져 나가는 문장입니다.따라서a=3,b=1a=2.b=2a=1.b=3a=0,b=4 따라서 b를 출력하므로 정답은 2번 입니다. 정보올림피아드 문제 풀이 리스트 정리

오늘은 학생이 c언어에서 문자열이 입력 되었을때...영문자 이거나 한글에서 맨 앞의 한글자만 출력해야 하는데 어떻게 하는지 묻길래 C언어에서 한글인지 영문인지 체크하는 방법을 알아 볼까 합니다. 먼저 다음과 같이 char Kor[] = "한글";char Eng[]="English";과 같이 변수를 선언하면서 데이터를 입력하면먼저 strlen(Kor) 을 출력해 보면 4 또는 6이 나오는 것을 확인하실 수가 있는데요.이것은 컴파일러마다 조금씩 다르기는 하지만 한글 같은 경우 2byte 혹은 3바이트를 사용하기 때문입니다.그렇다면 Kor[0] 을 출력하면 당연히 "한" 이라는 글자는 출력 되지 않을 것입니다. 먼저 이러한 원리를 이해하기 위해서는 ASCII 코드를 이해 해야 되는데요.이미지 출처 - http..

코드블럭(Code Block)을 사용하면 다음과 같이 철자를 몇개 입력하면 거기에 맞는 함수가 자동으로 나오게 됩니다.이렇게 나오면 거기에서 선택을 하거나 보면서 칠 수도 있는데... 저희 학생 중에 한명이 집에서 코드블럭을 설치했는데 이러한 자동완성 기능이 안된다고 물어 보네요.이러한 자동완성 기능이 안되면 무척이나 많이 불편한 부분이 있습니다.실제로 머리가 그렇게 썩 좋지 못한 저도 정말 많이 사용하는 함수들이나 그냥 사용하지 가끔가다 사용하는 함수는 철자도 정확하지 않아서 비슷한 단어를 써 보면서 그 함수를 찾는 경우가 많거든요. 사실 프로그래밍 하는 입장에서 이러한 함수들을 모두 다 외워야 하는 것은 정말 비효율적이지 않을까 생각 해 보게 되네요.이러한 함수들을 외우는 것 보다 좀더 좋은 알고리즘..

위와 같은 그림에서 교차점이 발생하는 경우는 a,c,d,h 인 경우 입니다. 이러한 두 선분의 교차점을 검사하는 방법으로는 다음과 같이 찾아 볼수가 있습니다. 1] 각 선분에 대해서 그 선분을 포함하는 양방향으로 무한한 연장선을 긋고 그 두 연장선의 일차방정식을 구한 후에 그로부터 교점을 계산한다. 그 교점이 원래의 두 선분상에 있으면 두 선분은 교차한다. 2] 위의 그림에서 a,c,d,h 인 경우를 살펴보면 다음과 같은 규칙을 찾을 수 있습니다. 1. 선분 AB를 기준으로 볼때 점 C 점 D가 서로 반대편에 존재 하는지 검사 선분 CD를 기준으로 볼때 점 A 점 B가 서로 반대편에 존재하는지 검사 2. 한 선분의 끝점이 다른 선분상에 존재 하는지 검사 3. 일직선상에 있으면서 한 선분의 끝점이 다른 선..

문제풀이)수평선에서 자기 자신과 가장 가까운 거리의 같은 색깔을 찾는 문제이다.가령 입력예 1 에서 0번의 색깔은 1이다 이것과 가장 가까운 색깔 1의 위치는 3 이다 따라서 0의 거리는 33번의 가장 가까운 거리는 0 번과 5번 중에서 가까운 5번이다 따라서 거리는 25번의 가장 가까운 거리는 3번 따라서 거리는 2 풀이1)색깔별로 바로 이전에 나온 위치를 저장해 놓고 자신의 위치에서 바로 이전의 같은색깔의 거리를 저장해 놓는다.만약 처음 나오는 경우는 무한값(최대값)을 설정해 놓는다.그리고 다음에 나오는 색상 (바로 이전에 나온 위치에서 바라보면 현재의 위치가 바로 이전에 나온 위치에서의 다음 위치이다.) 을 비교 하여 이전의 거리보다 짧다면 현재 위치의 거리를 갱신한다. 이렇게 하면 N번 만에 계산..

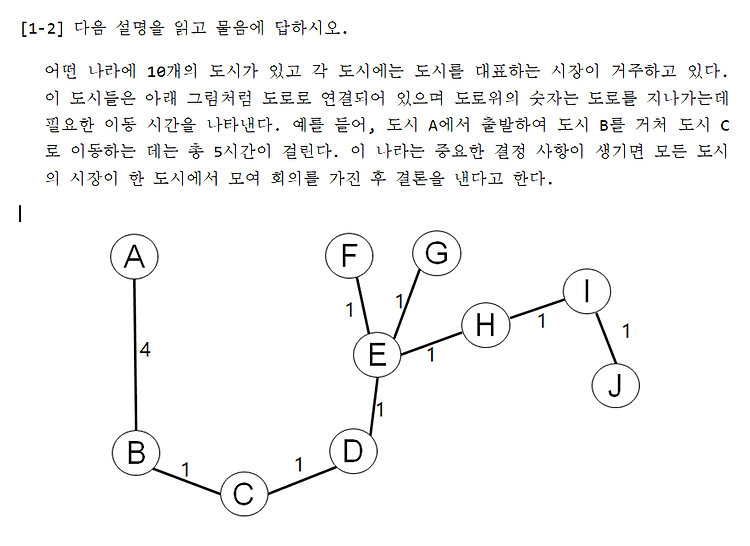
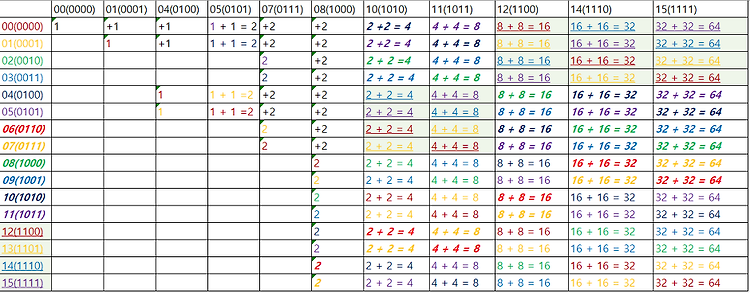
문제분석)이 문제는 모든 데이터를 찾아 가면서 가장 작은 값과 가장 큰 값을 찾아서 그 차이를 빼주면 됩니다. 일반적으로 가장 작은 값을 찾기 위해서는 min의 초기값은 가장 큰값보다 더 큰 수로 초기화 해 주어야 합니다. 여기서 학생들의 점수는 0~1000 사이라고 했으니 min 값을 1000 이상의 값으로 초기 화 한 후에하나하나 비교 하면서 min 보다 작은 값이 들어 오면 min 값을 갱신하는 형태로 처리하면 됩니다.max 값의 초기값은 가장 작은 값보다 더 작은 0 이하의 값으로 초기화 하면 됩니다.그리고 하나하나 비교하면서 max보다 큰 값이 나오면 max 값을 갱신하면 됩니다. 예제 소스는 네이버 블로그에 올렸습니다.하지만 예제 소스를 먼저 확인 하지는 마시고 먼저 충분히 고민한 후에 직접 ..