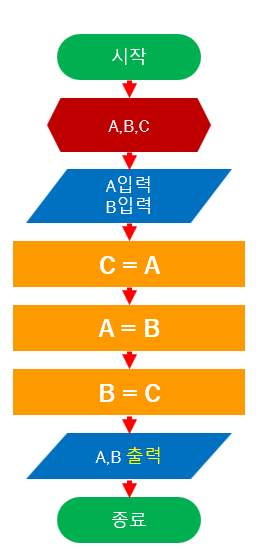
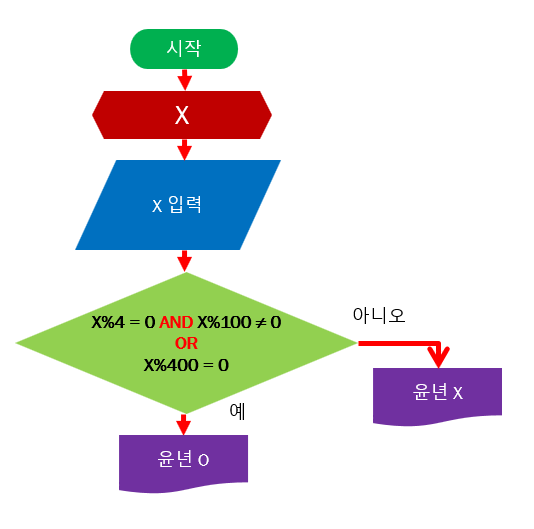
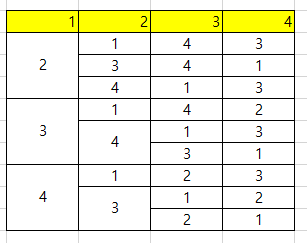
2024.02.27 - [강의자료/코딩으로 즐기는 수학] - 코딩으로 즐기는 수학 자료 목차 코딩으로 즐기는 수학 자료 목차1. 알고리즘과 순서도알고리즘이 무엇인지 살펴 본다알고리즘을 순서도로 표현해 보는 방법에 대한 이해이렇게 순서도로 표현한 알고리즘을 통해 간단한 프로그램을 엔트리로 구현해 본다.링wondangcom.tistory.com 목표작은 수와 큰 수를 비교하는 방법을 이해 한다.두 수의 값을 바꾸는 방법에 대해 이해한다.작은 수 부터 큰 수까지 반복하는 방법을 이해한다. 프로젝트 설명어느날 농부가 숲속에서 도끼를 잃어 버리고 도끼를 찾기 위해 숲속으로 들어 갔습니다.숲 속에서 헤매고 있는 농부에게 갑작스럽게 산신령이 나타났습니다. 산신령은 농부에게 두 수를 얘기해 주었습니다. 그리고 나무에 ..