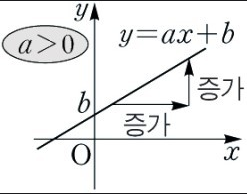
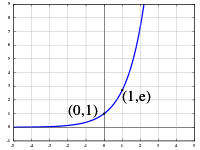
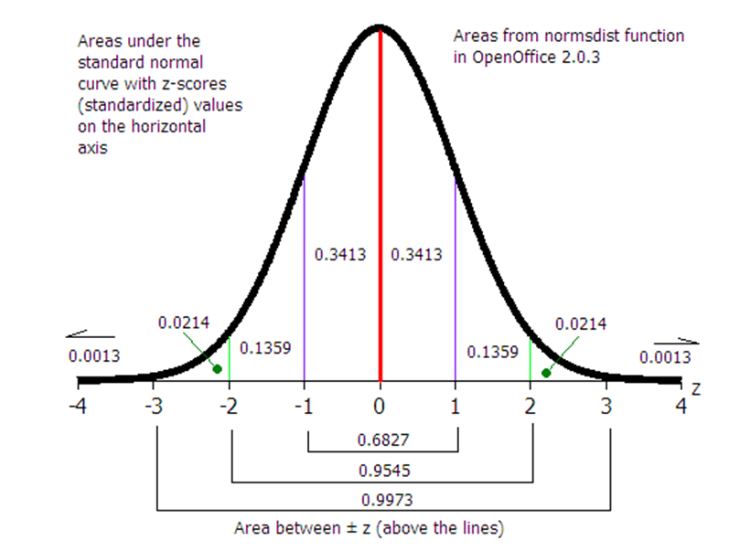
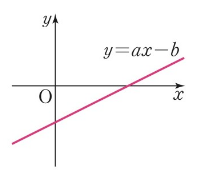시그모이드 함수를 알아보기 전에 선형 회귀에 대해 알아 보자. 1. 선형회귀 선형 회귀는 1차 함수로 표현할 수 있다. y=ax+b 여기서 a는 기울기(slope)이고 b는 절편(intercepter)이다. 딥러닝 분야에서는 기울기 a를 가중치를 의미하는 w로 표현하고 그리고 결과 y는 ˆy(y햇)으로 표기한다. 즉 선형 회귀 y=ax + b를 딥러닝 분야에서는 ˆy = wx + b와 같이 표현한다. 이러한 결과를 찾기 위해 전통적인 프로그램에서는 사람이 이러한 w와 b 의 값을 찾아 x를 입력받아 ˆy 을 출력하는 문제라면 딥러닝에서는 데이터를 입력 받아 w와 b 값을 찾아내는 모델을 만드는 것이 목적이다. 다음으로 이러한 선형회귀를 확장하여 분류모델(classification)을 만드는 과정을 이해해..