1. 누적분포란
평균이 0이고 표준편차가 1인 정규분포를 표준정규분포라고 한다.
평균이 0이고 표준편차가 1인 z점수 공식에 대입하면 z = x 가 된다.
따라서 표준 정규분포는 z 점수를 사용해 전체 데이터가 어떻게 분포되어 있는지 나타낼 수 있다.
예를 들어 표준정규분포에서 z 점수가 1.0 이내에 위치한 샘플은 전체의 약 68%에 해당한다. z점수 2.0 이내에 위치한 샘플은 95%에 해당한다.
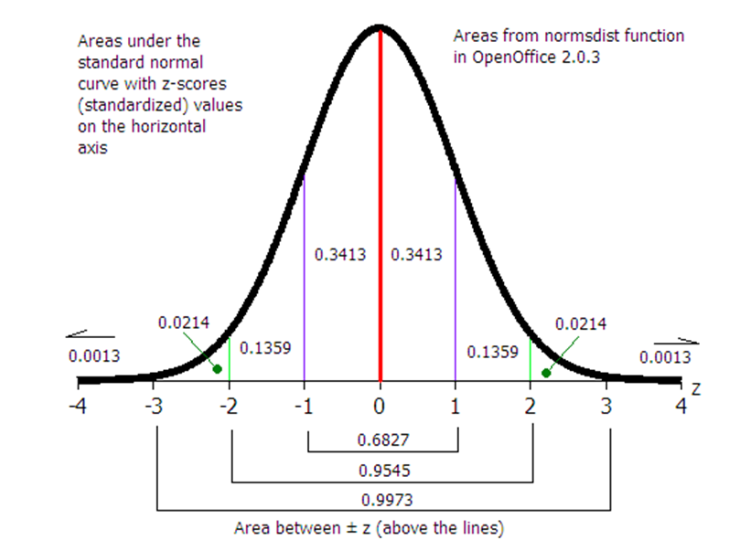
여기서 x축은 샘플값 또는 z점수, y축은 샘플의 등장 빈도 또는 밀도가 된다. 그럼 z 점수 1.5 이내에 있는 샘플의 비율은 얼마나 될까?
2. 누적분포 구하기
누적분포는 주어진 확률이 특정 값보다 작거나 같은 확률을 나타내는 값이다.
가령 표준정규분포에서 평균 0 까지 누적분포는 정확히 50%가 될것이다.
이러한 누적 분포를 구해주는 함수가 사이파이에 있다.
stats 모듈의 norm.cdf() 메서드는 누적된 분포를 반환해 준다.
직접 확인해 보면 다음과 같다.
stats.norm.cdf(0)0.5
만약 z 점수 1 이내의 비율을 구하려면 z 점수 1까지 누적분포에서 z 점수 -1 까지 누적분포를 빼면 된다.
이 값도 다음처럼 norm.cdf() 메서드로 손쉽게 구할 수 있다.
stats.norm.cdf(1.0) - stats.norm.cdf(-1.0)0.6826894921370859약 68% 라는 것을 알 수 있다.
이런 식으로 표준편차 2 이내의 비율도 다음과 같이 간단하게 계산 할 수 있다.
stats.norm.cdf(2.0) - stats.norm.cdf(-2.0)0.9544997361036416반대로 전체에서 특정 비율에 해당하는 z 점수를 구하려면 norm.ppf() 메서드를 사용한다.
예를 들어 90% 누적분포에 해당하는 z점수는 다음처럼 얻을 수 있다.
stats.norm.ppf(0.9)1.2815515655446004
참고] 한빛미디어 - 혼자공부하는데이터분석
'강의자료 > 인공지능수학' 카테고리의 다른 글
| [인공지능수학] 신뢰구간(Confidence Interval) (17) | 2023.02.24 |
|---|---|
| [인공지능수학] 중심극한정리 (17) | 2023.02.10 |
| [인공지능수학] 표준점수 (18) | 2023.01.27 |
| [인공지능수학] 호도법/도수법 실습하기 (20) | 2023.01.20 |
| [인공지능수학] 등차수열의 합 실습하기 (19) | 2023.01.06 |