다음의 데이터를 참고하여 월 매출과 관련이 깊은 지표를 찾아 봅니다.
| 데이터 종류 | 1월 | 2월 | 3월 | 4월 | 5월 | 6월 | 평균 |
| 매출 | 2500 | 4000 | 2000 | 5500 | 3500 | 4500 | 3670 |
| 상품구입비 | 2000 | 1500 | 3000 | 1000 | 1500 | 1500 | 1750 |
| 광고비 | 200 | 100 | 400 | 300 | 200 | 200 | 233 |
| 조회수 | 180 | 270 | 160 | 620 | 320 | 390 | 323 |
| 결제수 | 10000 | 20000 | 8000 | 40000 | 2800 | 30000 | 22700 |
| 체류시간 | 69 | 88 | 68 | 180 | 120 | 77 | 100 |
위의 데이터를 가지고 어떤 데이터가 다른 데이터와 관련이 깊은지 상관관계를 찾아 봅니다.
상관관계는 공분산을 구해보면 알 수 있습니다.
여기서 공분산이 무엇인지 살펴 보겠습니다.
공분산은 공+분산의 의미인데 여기서 공은 공동체할때 사용하는 공으로 함께,여럿을 뜻합니다.
따라서 공분산은 여럿으로 구한 분산을 말합니다.
공분산을 구하는 공식은 다음과 같습니다.
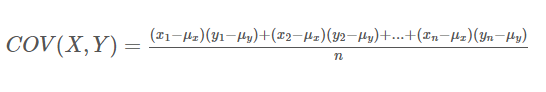
여기서 분자의 첫항

위의 식으로 다음과 같은 성질을 알아 낼 수 있습니다.
1) x1이 x의 평균보다 크고 y1도 y의 평균보다 크면 양수가 됩니다.
2) x1이 x의 평균보다 작고 y1도 y의 평균보다 작으면 양수가 됩니다.
3) x1이 x의 평균보다 크고 y1도 y의 평균보다 작으면 음수가 됩니다.
4) x1이 x의 평균보다 작고 y1도 y의 평균보다 크면 음수가 됩니다.
따라서
공분산의 값이 양수라면 x가 평균보다 클때 y가 평균보다 크거나, x가 평균보다 작을때 y가 평균보다 작은 경우가 많다고 할 수 있습니다.
산점도를 그려보면 다음과 같이 우상향 그래프 입니다.
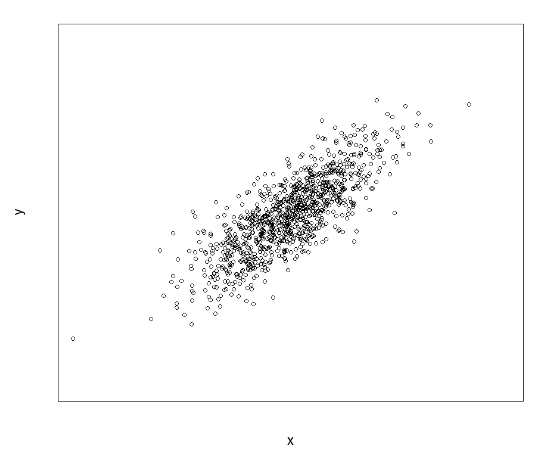
공분산이 음수라면 산점도 그래프는 우하향 그래프가 나오고 공분산이 0 이라면 한 점에 밀집하는 형태로 나오게 됩니다.
공분산은 크기와 부호를 갖는데요, 공분산의 부호는 두 변수의 분포상태를 알려 주며 크기는 클수록 길게 분포하게 됩니다.
또한 공분산은 두 변수간 평균적은 편차의 곱으로 나타낼 수 있습니다.

그럼 위의 데이터에 대한 공분산을 구해 보도록 하겠습니다.
여기서는 어림잡아 관계가 있을 것 같은 데이터에 대해서만 계산 하도록 하겠습니다.
매출액은 광고비나 상품조회수와 관계가 있을 것 같아서 월매출(R),광고비(A),상품조회수(P) 에 대해 공분산Cov(R,A)와 Cov(R,P)를 계산해 보도록 하겠습니다.
| 1월편차 | 2월편차 | 3월편차 | 4월편차 | 5월편차 | 6월편차 | 표준편차 | |
| R | -11.7 | 3.3 | -16.7 | 18.3 | -1.7 | 8.3 | 11.8 |
| A | -0.33 | -1.33 | 1.67 | 0.67 | -0.33 | -0.33 | 0.943 |
| P | -143 | -53 | -163 | 297 | -3 | 67 | 154 |
Cov(R,A)=( (-11.7 * -0.33) + (3.3 * -1.33) + .... + (8.3 * -0.33) ) / 6 = -3.056
Cov(R,P)=( (-11.7 * -143) + (3.3 * -53) + ... +(8.3 * 67) ) /6 = 1703
공분산의 내용으로
월매출과 광고비는 음의 상관관계
월매출과 상품조회수는 양의 상관관계가 있는 것을 알 수 있습니다.
그렇다면 이 상관관계들은 얼마나 강한 관계일까요?
우선 공분산 값만 보면 상품조회수의 값이 월등히 크기 때문에 Cov(R,P)가 크게 나오는데요~
이것은 단위 자체가 다르기 때문에 이 둘을 비교하는 것은 의미가 없습니다.
그래서 도입된 것이 상관계수(Correlation coefficient) 입니다.
상관계수는 다음과 같이 구합니다.

이때 상관계수는 각각의 표준편차로 나누어 단위를 없애 버린 값으로 -1~1 사이의 수가 나오게 됩니다.
이러한 과정을 정규화라고 부릅니다.
그러면 다음 상관관계를 구해 봅니다.
Corr(R,A) = -3.056/(11.8 * 0.943) = -0.2746
Corr(R,P) = 1703/(11.8*154) = 0.9372
상관계수는 1에 가까울 수록 양의 관계가 강하고 -1에 가까울 수록 음의 관계가 강합니다.
일반적으로 상관계수가 절대값 0.7보다 클 때 상관관계가 강하다고 말하는데요.
위의 결과로 매출과 조회수의 상관관계가 강한 것을 알 수 있었습니다.
| 인공지능에서 활용 |
인공지능에서 데이터를 분석 할 때 직관적으로 분석하기 어려울 만큼의 대량의 데이터가 있다면 컴퓨터를 이용하여 그들의 상관계수를 계산하면서 상관관계가 강항 조합을 찾아 낼 수 있습니다.
이런 과정을 거치면서 사람이 미처 발견하지 못했던 숨은 관계나 데이터의 특장을 찾을 수 있어 데이터를 유용하게 활용할 수 있게 됩니다.
참고]
프리렉 - 인공지능을 위한 수학
공분산 : https://hsm-edu.tistory.com/1266
공분산이란 무엇인가 (정의와 의미)
역사적 정황을 정확히 알 수는 없지만 공분산은 분산에서 유래된 개념인 것 같습니다. 분산을 먼저 발견하고, 이후에 공분산을 떠올린 것입니다. 공분산은 공+분산인데, 여기서 공은 함께,
hsm-edu.tistory.com
[인천 서구 원당컴퓨터학원]
'강의자료 > 인공지능수학' 카테고리의 다른 글
| [인공지능수학] 경사하강법으로 학습하는 방법 알아 보기 (6) | 2022.10.06 |
|---|---|
| [인공지능수학] 표준편차 (5) | 2022.08.10 |
| [인공지능수학] 확률 (7) | 2022.04.04 |
| [인공지능 수학] 행렬 (11) | 2022.03.25 |
| [인공지능수학] 미분 (7) | 2022.02.24 |