| 목표 |
- 벡터가 무엇인지 살펴보고 인공지능 프로그램에서 어떻게 사용되는지 살펴 봅니다.
| 벡터란 |
- 벡터는 크기와 방향을 갖춘 양을 말합니다.
- 벡터는 공간에서 한점을 나타냅니다.(1차원 상의 점은 벡터 보다는 스칼라라고 부릅니다.)

1을 벡터라고 부르기 보다는 스칼라라고 부른다. - 2차원 상의 점을 (x,y)로 표현되는데 원점에서 부터 공간상의 한 점 까지의 상대적 위치를 벡터라고 이해하면 됩니다.

- 인공지능에서는 n차원상의 공간에서의 한 점으로 표현을 합니다.(인공지능에서는 대부분 큰 차원의 벡터를 다루게 됩니다.)
- 벡터에 숫자(스칼라)를 곱해주면 길이만 변합니다.
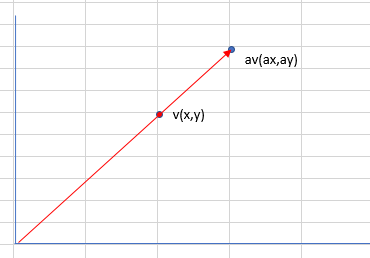
a가 1보다 크면 길이가 늘어나고,a가 음수이면 반대 방향이 됩니다. - 이러한 여러개의 데이터를 한 줄에 담아 낼 수 있게 만든 것을 벡터라고 합니다.
- 벡터는 다음과 같이 표현 합니다.

| 벡터의 덧셈과 뺄셈 |
- 벡터끼리 덧셈과 뺄셈은 서로 대응하는 성분끼리 덧셈 뺄셈을 합니다.
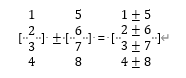
- 하지만 위의 벡터에서 행의 크기가 다르면 덧셈과 뺄셈 계산을 하지 못합니다.( 인공지능에서 두 벡터의 덧셈 뺄셈이 이루어지는 경우 서로 다른 차원 인 경우 덧셈 뺄셈 연산이 불가능합니다.)
| 벡터의 내적 |
- 벡터의 내적은 서로 대응하는 성분끼리 곱한 다음 그것들을 모두 더한 값입니다.
- 벡터의 내적의 기호는 <a,b> 로 사용 됩니다.
- 벡터와 벡터의 내적은 벡터가 아니라 스칼라가 됩니다.
- 벡터의 내적 계산방법

- v1=(2,1),v2=(1,3) 인 두 벡터의 내적의 크기는 다음과 같이 구할 수 있습니다.
<v1,v2> = 2 * 1 + 1 * 3 = 2 + 3 = 5 - 이때 벡터 a와 b가 이루는 각이 θ 일때 기하학적인 특징으로 다음과 같이 정의 할 수 있습니다.
<a,b> = ||a||*||b||*cosθ 단,||a|| 는 a의 유클리드 거리를 의미합니다. - v1=(2,1),v2=(1,3) 인 두 벡터의 내적의 크기를 기하학적인 특징으로 구해 보면 두 벡터가 이루는 각도 θ=45° 이므로 다음과 같이 구할 수 있습니다.
<a,b>=||a||*||b||*cosθ = √(4+1) * √(1+9) * cos45° = √5 * √10 * √2/2 = 5 - 이때 내적은 정사영된 벡터의 길이과 관련이 있습니다.

- 정사영 된 벡터는 코사인 법칙에 의해 ||a||cosθ 가 됩니다.
- 내적은 정사영의 길이를 벡터 b의 길이 ||b|| 만큼 조정한 값입니다.

- 이처럼 내적은 머신러닝에서 두 벡터의 유사도가 어느정도 비슷한 방향으로 가는지를 체크할 때 사용합니다.
※ 벡터의 내적으로 두 벡터의 각도를 알 수 있는데
A벡터와 B벡터의 각도를 다음과 같이 알 수 있다.

| 벡터의 노름(Norm) |
- 벡터의 노름(Norm) 은 원점에서부터의 거리를 말합니다.

- L1 노름 - 벡터 성분의 절댓값을 모두 더해 구해지는 값 ( 위의 a 의 L1 노름은 x축 이동거리 4 + y축 이동거리 3 = 7)
- L2 노름 - 벡터의 유클리드 거리로 구해지는 값 (위의 a의 L2 노름은 유클리드 거리인 5)
- 여기서 L1노름을 맨하탄 거리라고도 부릅니다. 3차원 이상의 L1노름을 구할때는 각 성분들의 절댓값을 모두 구한 다음 모두 더하면 됩니다.
a에 대한 L1노름 = ||a||1 = |a1| + |a2| + ... |an| - L2 노름은 유클리드 거리인 직전으로 움직인 거리를 구하는 방법으로 3차원 이상의 공간에서도 똑같이 적용
a에대한 L2노름 ||a||2 = √(a1^2 + a2^2 + ... an^2) - L1과 L2의 차이는 노름의 종류에 따라 기하학적 성질이 달라집니다.

| 두 벡터 사이의 거리 |
- L1,L2 노름을 이용해 두 벡터 사이의 거리를 계산 할 수 있습니다.
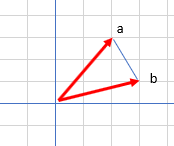
- 두 벡터 사이의 거리를 계산할 때는 벡터의 뺄셈을 이용합니다.

- 뺄셈을 하면 원점에서의 벡터가 생성됩니다.
| 벡터 사이의 각도 계산 |
- L2 노름을 이용하여 벡터 사이의 거리를 이용하여 각도도 계산 할 수 있습니다.

- ||a-b||2 = ||b-a||2 입니다.
- 제2 코사인 법칙을 살펴 봅니다.
- a2 = b2 + c2 - 2bcCosA
- b2 = c2 + a2 - 2caCosB
- c2 = a2 + b2 - 2abCosC
- cosθ = (||a||22 + ||b||22 - ||a-b||22) / (2 * ||a||2 * ||b||2)
- 여기서 분자를 쉽게 계산하는 방법이 바로 내적입니다. 내적은 두 벡터의 성분곱을 취한 후 그 성분곱을 더해 주는 것이 내적이며 분자에 해당하는 것이 내적입니다.
cosθ = (2<a,b>) / (2 * ||a||2 * ||b||2) = <a,b>/(||a||2 * ||b||2)
| 벡터 를 프로그램에서 표현 |
3차원 공간의 벡터 a = (x1,y1,z1)

와 같이 리스트로 표현 되며 n차원 공간의 벡터도 리스트로 표현이 가능합니다.
| 인공지능에서의 활용 |
- 인공지능에서 L1노름과 L2노름은 선형회귀 모델의 정규화 항에서 사용합니다.
- 내적은 머신러닝에서 두 벡터이 유사도가 어느정도 비슷한 방향으로 가는지를 체크할 때 사용합니다.
- 인공지능에서는 언어를 처리하기 위해서 단어들을 마치 벡터처럼 취급하는 방법이 있습니다. word2vec 가 바로 이 개념을 사용하는데 단어를 일렬로 늘어 놓아 벡터를 만듭니다.
- 이렇게 만들어진 벡터는 일반적인 벡터 연산처럼 단어들의 덧셈과 뺄셈의 기능도 수행할 수 있습니다.
사업자 정보 표시
원당컴퓨터학원 | 기희경 | 인천 서구 당하동 1028-2 장원프라자 502호 | 사업자 등록번호 : 301-96-83080 | TEL : 032-565-5497 | Mail : icon001@naver.com | 통신판매신고번호 : 호 | 사이버몰의 이용약관 바로가기
'강의자료 > 인공지능수학' 카테고리의 다른 글
| [인공지능 수학] 행렬 (11) | 2022.03.25 |
|---|---|
| [인공지능수학] 미분 (7) | 2022.02.24 |
| [인공지능수학] 유클리드 거리 (9) | 2022.02.09 |
| [인공지능수학] 삼각함수 (9) | 2022.01.25 |
| [인공지능수학] 활성화 함수 (6) | 2022.01.18 |