
문제풀이)
2학년부터 4학년 학생중 학점이 3.0 이상인 학생은
2학년 - 22명
3학년 - 28명
4학년 - 18명
2학년 3.0 이상인 학생이 3학년 3.0 또는 4학년 3.0 이상인 학생과 중복 되는 경우가 없으므로
경우의 수는 22 + 28 + 18 = 68 가지 이다.


[문제풀이]

문제풀이)
1) 한가지만 선택하는 경우이므로 한가지를 선택하면 다른 것을 선택 할 수 없다. 따라서 합의 법칙에 해당한다.
5+2+4+3 = 14
2) 각각 하나씩 선택을 해야 하므로 곱의 법칙에 해당한다. 5 * 2 * 4 * 3 = 120


문제풀이)
첫째자리에 4가지를 선택 할 수 있다.
둘째자리에 첫째자리에서 선택한 1가지를 제외한 3가지를 선택할 수 있다.
셋째 자리에 첫째자리와 둘째 자리에서 선택한 2가지를 제외한 2가지를 선택할 수 있다.
따라서 4 * 3 * 2 = 24


문제풀이)
1) 처음 온 학생이 5권중에서 한권을 선택(5가지)
두번 째 온 학생이 남은 4권중에선 한권을 선택(4가지)
세번 째 온 학생이 남은 3권 중에서 한권을 선택(3가지)
따라서 5 * 4 * 3 = 60가지
2) 1)과 동일한 방법에 의해 5 * 4 * 3 * 2 * 1 = 120가지
3) 어느 학생도 책을 가져 가지 않았다고 하면 안가져 간 경우 1가지
5P0 = 5!/(5-0)!=1

문제풀이)
1) 2를 첫번째 자리에 선택을 하면 두번째 자리는 나머지 6가지, 셋째 자리는 나머지 5가지, 넷째자리는 나머지 2가지 이므로 6*5*4 = 120가지
공식에 대입하면 6P3 = 6!/(6-3)! = 6*5*4 = 120 가지
2) 짝수가 되기 위해서는 마지막 자리가 0,2,4,6 인 경우
마지막이 0 인 경우 앞에서 부터 6*5*4 = 120가지
마지막이 2,4,6 인 경우 각각 첫번째 자리는 0과 마지막 선택한 것을 제외하므로 5가지,둘째자리 5가지, 셋째자리 4가지 이므로 5 * 5 * 4= 100가지
따라서 120 + 3*100 = 420가지
3) x61x 에서 이미 두개가 나왔기 때문에 5개의 숫자 중에서 2개를 선택하는 경우의 수임
하지만 맨 앞에는 0 이나올 수 없으므로 첫째자리에 4가지 숫자가 올수 있고 마지막은 선택된 3가지를 제외한 4가지가 올 수 있으므로 4 * 4 = 16가지


문제풀이)
첫째자리에 4개의 숫자가 나올수 있다
둘째자리에 4개의 숫자가 나올수 있다
셋째자리에 4개의 숫자가 나올수 있다
따라서 4∏3 = 4*4*4 = 64

문제풀이)
1) 2xxx 이므로 7*7*7=343 가지
2) 짝수는 마지막자리가 0,2,4,6 인 경우이므로 4*(6 * 7 * 7) = 4 * 294 = 1176
3)x61x 이므로 6 * 7 = 42 가지


문제풀이)
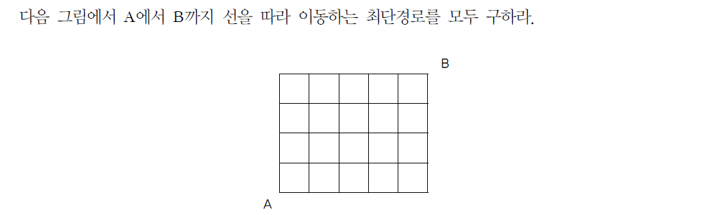
문제풀이)
[출처] 컴퓨팅 사고력을 키우는 이산수학
[역대 기출문제]
https://docs.google.com/forms/d/e/1FAIpQLScl_vpVyyRzSlQWjYkd_fVI1D0fXpshXXRd_ovh64e2DYA2Sw/viewform
8-1. 순열에관한문제(곱의법칙,합의법칙)-초등부
docs.google.com
https://docs.google.com/forms/d/1_l-iQud1i_lMWowpay4Q-kBO7_X9H_nEGY9DPPp5km8/edit
8-2. 순열에관한문제(곱의법칙,합의법칙)-중고등부
docs.google.com
'강의자료 > 이산수학문제풀이' 카테고리의 다른 글
| [정보올림피아드대비]9. 나누어 떨어짐을 이용하는 문제(배수판정법) (13) | 2022.05.13 |
|---|---|
| [정보올림피아드대비]8.조합에관한문제 (13) | 2022.05.06 |
| [정보올림피아드대비]6.숫자로 진 만들기(복면산연산) (10) | 2022.04.14 |
| [정보올림피아드대비]5. 기하문제-평면 (11) | 2022.04.07 |
| [정보올림피아드 대비]4. 기하 문제-선분 (5) | 2022.03.17 |

