1. 도형의 둘레
- 사각형의 둘레 구하기

사각형 둘레는 a + a + b + b 이므로 2 * (a+b)
- 삼각형의 둘레 구하기

삼각형의 둘레는 a + b + c
※ 여기서 피타고라스 정리에 의해 직각 삼각형의 빗변 c의 제곱은 다른 두변 a,b의 제곱의 합과 같다
증명)

이렇게 연장선을 그려서 하나의 정사각형을 만들어 보자.
CDFH 의 넓이 = 삼각형 ABC의 넓이 * 4 + 사각형 AEGB의 넓이
CDFH 의 넓이 = (a+b)^2 = a^2 + 2ab + b^2
사각형 AEGB의 넓이 = c * c
삼각형 ABC의 넓이 = a * b / 2 이므로
a^2 + 2ab + b^2 = c * c + 4 * a * b / 2
따라서 a^2 + b^2 = c^2
- 원의 둘레
원의 둘레는 원의 반지름과 비율이 일정합니다.

위의 그림과 같이 원을 잘게 잘라서 이어 붙인다고 하면 원의 둘레의 1/2 이 밑변이 되고 반지름이 높이인 직사각형을 만들 수 있는데요.
이때 밑변을 만드는 원의 둘레에 원주율을 곱해 주면 되는데 그 값은 일반적으로 3.14 로 계산합니다.(근사치값)
따라서 원의 둘레는 2 * 3.14 * 반지름 과 같이 계산합니다.
2. 도형의 넓이
- 사각형의 넓이 구하기 - 높이(h) * 너비(a)

- 삼각형의 넓이 구하기 - (높이(h) * 너비(a)) / 2
그 외에도
- 각을 이용하여 구하는 공식 중에 다음과 같은 공식이 있다.(단, 정보올림피아드 문제 유형에는 없다.)

위의 그림에서 높이를 bsin(θ) 로 표현 할 수 있다.
따라서 넓이 = a * bsin(θ) / 2
- 세 변을 이용하여 넓이를 구하는 공식은 코사인 법칙을 이용해서 넓이를 구하는 공식이 있다.(단, 정보올림피아드 문제 유형에는 없다. - 단 고등부라면 향후에 나올 가능성이 있다는 점에 유의하자.)

코사인 법칙을 이용해서 유도를 하면 s=(a+b+c)/2 라는 임의의 수라고 가정하면
삼각형의 넓이 = √(s(s-a)(s-b)(s-c)) 로 표현할 수 있다.
- 세 꼭지점의 좌표로 넓이를 구하는 방법 (기하 알고리즘에서 다각형의 넓이를 구하는 방법에서 자주 나오는 유형이다.)






이렇게 유도한 삼각형 넓이를 구하는 공식을 외우는 방법은 다음과 같다.

쌍끼리 곱한 후 빨간색은 + 부호 파란색은 - 부호를 붙여서 곱해 주면 다각형의 넓이 구하는 공식이 됩니다.
- 평행사변형의 넓이 구하기 - (높이(h) * 너비(a))
- 사다리꼴의 넓이 구하기 - (밑변(b)+윗변(u)) * 높이(h) / 2

- 마름모꼴의 넓이 구하기 - AC의 길이 * DB의 길이 / 2

- 원의 넓이 구하기

여기서 원주란 원의 둘레의 길이를 의미하는데 원주는 원의 반지름의 길이의 비율이 일정합니다.
이때 이 비율을 원주율이라고 합니다.
이 원주율은 약 3.14 이고 π(파이) 라고 합니다.
따라서 원의 넓이는 반지름 * 원주의 1/2 이므로 원주율 = 원주 / 지름 = 3.14 이므로
원주는 3.14(π) * 지름(2*반지름) 입니다.
따라서 반지름(r) 인 원의 넓이 = r*r*π 입니다.
- 부채꼴의 넓이 구하기
부채꼴은 원의 일부분이기 때문에 원 하나의 몇분의 몇인지만 판단하면 됨
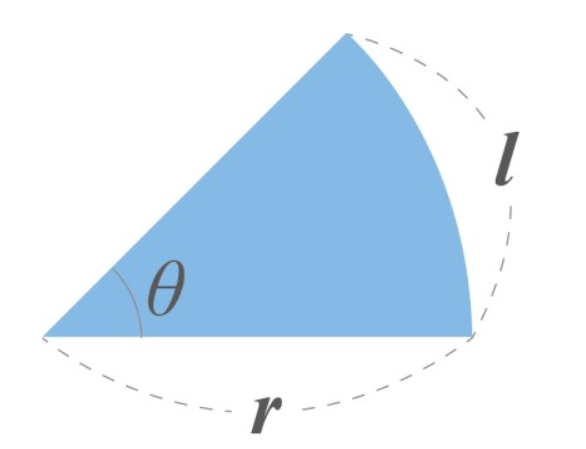
원의 각도는 360도 이므로 원의 넓이 r * r * 3.14 에서 Θ/360 를 곱해 주면 된다.
호의 길이 l 을 아는 경우에는 (r*l)/2 로 계산하기도 합니다.
l=2*3.14*r*Θ/360 이므로
넓이 = r * r * 3.14 * Θ/360 = 1/2*(2*3.14* r * r * Θ/360)=1/2*r*(2*3.14*r*Θ/360)이므로
넓이 = 1/2 * r * l
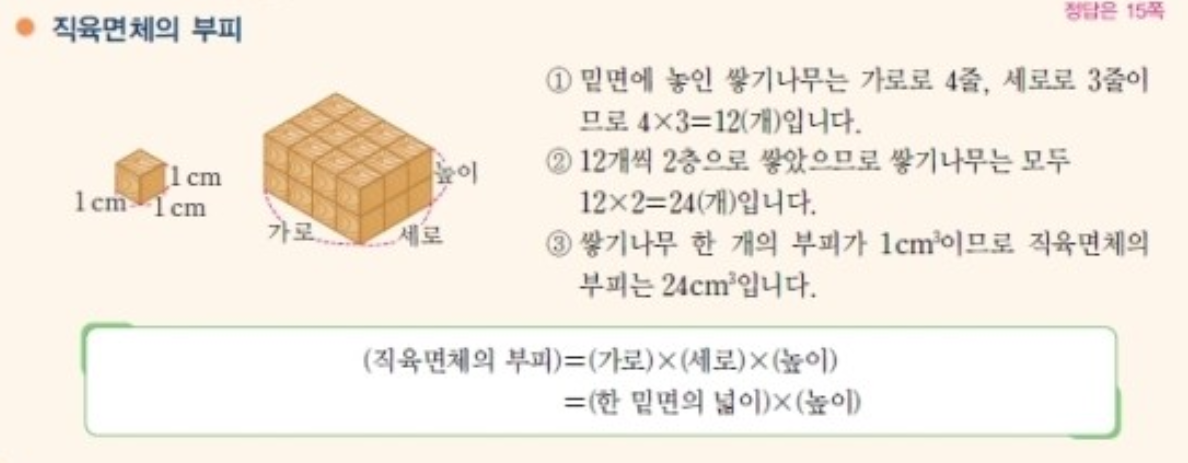
- 직육면체의 겉넓이 구하기

- 직육면체의 부피 구하기
- 원기둥의 겉넓이 구하기
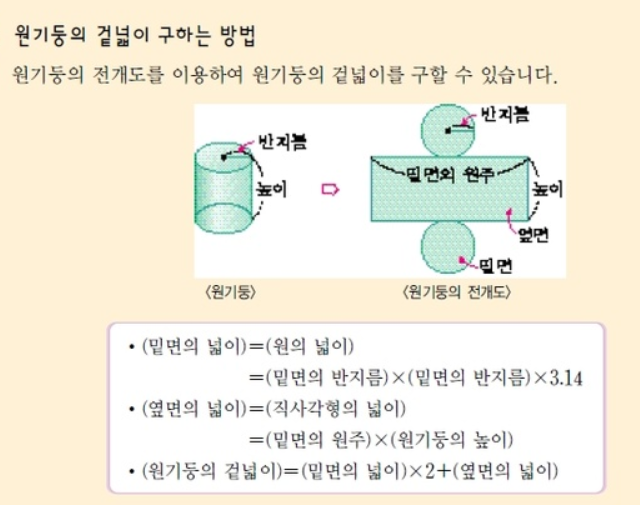
원기둥의 전개도를 확인하면 높이 * 밑면의 원주 와 밑면의 원과 위면의 원으로 이루어져 있음을 확인할 수 있습니다.
여기서 밑면의 원주 = 2*π*r 입니다.
- 원기둥의 부피 구하기
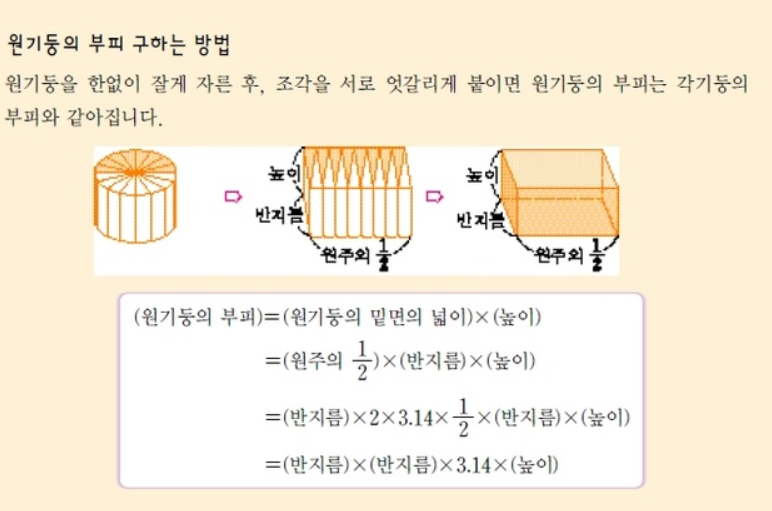
- 원기둥을 잘게 자른 후에 조각을 서로 엇갈리게 붙이면 원주의 1/2 , 반지름, 높이인 각기둥의 부피와 같아 지는 것을 확인 할 수 있습니다.
원기둥의 부피 = r * r * 3.14 * 높이
3. 도형의 내각의 합
- 삼각형의 내각의 합 : 180도
증명)
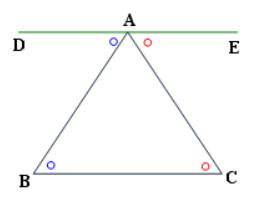
ABC의 삼각형에 BC와 평행한 DE의 선분을 그었을때 위와 같은 그림이 됩니다.
따라서 DAB 와 ABC의 엇각의 크기가 같고 EAC와 ACB의 엇각의 크기는 같기 때문에...
각 DAB + 각ABC + 각CAE = 180 이 되는것을 확인 할 수 있습니다.
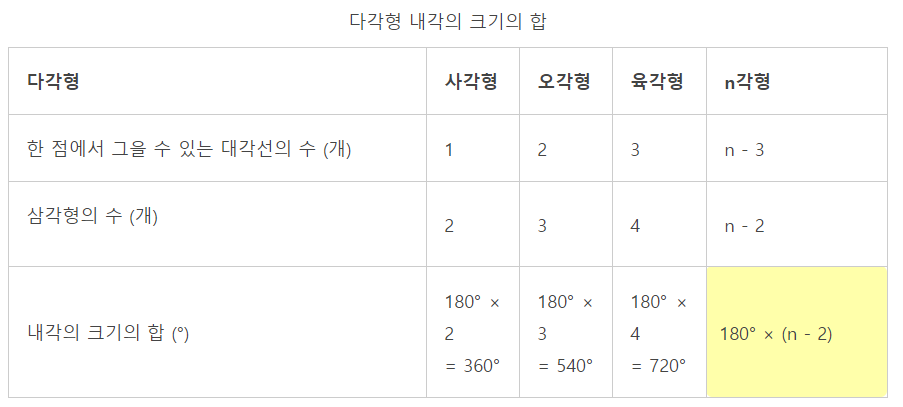
- 다각형의 내각의 합 : n각형 = (n-2)*180
증명)
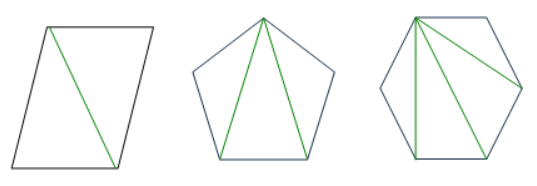
삼각형의 내각의 합이 180도가 되기 때문에 다각형을 위와 같이 삼각형으로 쪼갤 수 있는데 이렇게 쪼개 보면 n 각형은 n-2개의 삼각형으로 쪼갤수 있는것을 확인할 수 있다.
4. 도형 색칠하기
4색정리로 알려져 있는 이 문제는 평면을 유한개의 부분으로 나누어 각 부분에 색을 칠할 때, 서로 맞닿은 부분을 다른 색으로 칠한다면 네가지 색으로 충분하다는 정리이다.
이 문제는 지도에서 서로 맞닿은 지역에 다른 색을 칠한다는 것에서 착안해 만들어졌다.
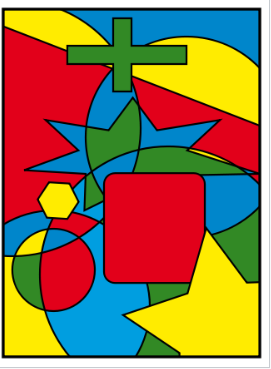
이러한 4색정리는 모든 평면 그래프의 꼭짓점이 많아야 4가지 색만을 이용하여 인접한 꼭짓점들이 같은 색을 가지지 않도록 칠할수 있는 가 하는 것에서 출발했다.
[역대 기출문제유형]
https://docs.google.com/forms/d/e/1FAIpQLSe1ldynHQSTCvBHvg2ay9_Zwuryu9zcbaPXJsRcj568jBqeXg/viewform
6-1. 기하문제 - 평면(초등부)
docs.google.com
https://docs.google.com/forms/d/e/1FAIpQLScPESMXYhmqsejBGKPYB-15QzFoPfxBAlFWGNuVuWXh3L-gjQ/viewform
6-2. 기하문제 - 평면(초등부)
docs.google.com
https://docs.google.com/forms/d/e/1FAIpQLScDgrJQDRxWhdulj_9b1vq73dGQZdeYIff68HSbGiOXRxLwyw/viewform
6-3. 기하문제 - 평면(중고등부)
docs.google.com
'강의자료 > 이산수학문제풀이' 카테고리의 다른 글
| [정보올림피아드대비]7. 순열에 관한 문제(곱의법칙,합의법칙) (9) | 2022.04.26 |
|---|---|
| [정보올림피아드대비]6.숫자로 진 만들기(복면산연산) (10) | 2022.04.14 |
| [정보올림피아드 대비]4. 기하 문제-선분 (5) | 2022.03.17 |
| [정보올림피아드 대비]3. 속도와 거리 문제 (15) | 2022.02.18 |
| [정보올림피아드 대비]2. 수열을 응용한 문제(등차수열,등비수열 외) (11) | 2022.01.21 |