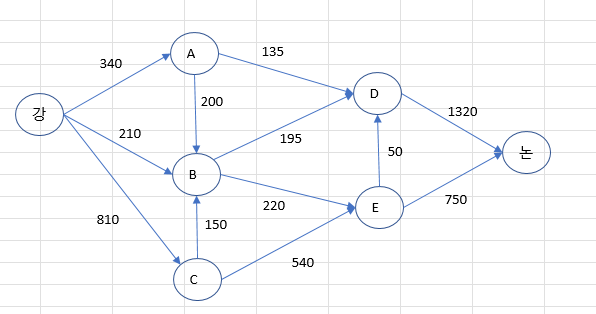
원당이는 한빛도서에서 책을 하나 구매했는데 홈페이지에 ISBN 코드를 인증 받으면 포인트를 준다고 합니다. 그런데 어린 동생이 ISBN의 가장 마지막 자리를 사인펜으로 낙서를 해 놓는 것 때문에 ISBN 코드로 인증을 받지 못하게 되었는데 인터넷으로 ISBN 에 대해 검색을 하니 ISBN 에 대해 다음과 같이 설명이 되어 있습니다. ISBN(International Standard Book Number)는 국제적으로 책에 붙이는 고유한 식별자이다. ISBN체계는 원래 1966년 영국에서 "표준 도서 번호"(SBN)라는 이름으로 만들어졌고, 1970년 국제 표준화 기구에 의해 ISO 2108이라는 표준으로 채택되었다. 본래 ISBN은 10자리였지만 2007년 1월 1일 이후부터는 유럽상품번호(EAN)에 맞..