| 부분합 알고리즘이란? |
N명의 시험 성적을 내림차순으로 정렬해 둔 score[] 가 있다고 하면 여기서 우리는 a등에서 b등까지의 평균을 구하려고 한다.
가장 간단한 알고리즘으로는 a등부터 b등까지의 합을 구한 다음 b - a + 1 로 나누는 것이다.
하지만 이렇게 구하는 횟수가 빈번해진다고 하면 1회를 구할 때마다 최대 N번씩 반복하게 된다.
이럴 때 유용하게 사용하는 것이 부분합(Partial sum)이다.

위와 같이 psum 테이블을 미리 구해 놓는다고 하면 2번지 부터 4번지까지의 부분합을 구하려고 하면
psum[4] 는 0,1,2,3,4 의 모든 합이기 때문에 여기서 0,1 의 값을 빼면 2번지부터 4번지 까지의 부분합이 된다.
따라서 psum[4] - psum[1] 의 값이 2번지 부터 4번지까지의 부분합이 된다.
여기서 주의 할 점은 0번지 부터 4번지까지의 합을 구하는 경우 psum[4] - psum[-1] 이 되는 경우가 발생하는데 이러한경우 -1 번지 위치를 처리해야 되는 부분에 유의해야 한다.
| 부분합 계산하기 |
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
#include <iostream>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
vector <int> partialSum(const vector<int> &a)
{
vector <int> ret(a.size());
ret[0]=a[0];
for(int i=1;i<a.size();++i)
{
ret[i]=ret[i-1]+a[i];
}
return ret;
}
int rangeSum(const vector<int> &psum,int a,int b)
{
if(a==0) return psum[b];
else return psum[b]-psum[a-1];
}
int main()
{
int n;
vector <int> psum;
vector <int> num;
cin >> n;
for(int i=0;i<n;i++)
{
int a;
cin >> a;
num.push_back(a);
}
psum = partialSum(num);
int a,b;
int m;
cin >> m;
for(int i=0;i<m;i++)
{
cin >> a >> b;
cout << rangeSum(psum,a,b) << endl;
}
return 0;
}
|
cs |
| 2차원 부분합 계산하기 |
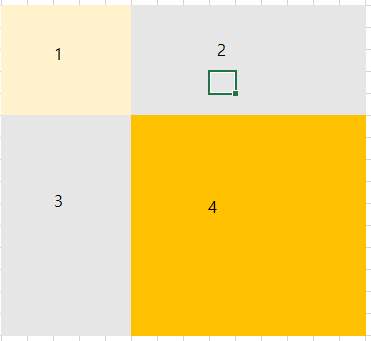
4번 영역의 부분합을 구하려고 하면 먼저 모든 구간합을 구한 다면 4번 오른쪽 하단 위치가 전체 영역의 합이 된다.
이 안에는 1번영역 + 2번 영역 + 3번 영역의 합이 포함이 되어 있게 된다.
따라서 3번 오른쪽 하단 영역 과 2번 오른쪽 하단 영역의 합을 뺀다고 하면 1번 영역의 합이 2번 빠지게 된다.
그러므로 다시 1번 영역의 합을 구해 주면 된다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
|
#include <iostream>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
// 어떤 2차원 배열 A[][]의 부분합 psum[][]이 주어질 때,
// A[y1,x1]과 A[y2,x2]를 양 끝으로 갖는 부분 배열의 합을 반환한다.
int gridSum(const vector< vector<int> >& psum, int y1, int x1, int y2, int x2){
int ret = psum[y2][x2];
if(y1>0) ret -= psum[y1-1][x2];
if(x1>0) ret -= psum[y2][x1-1];
if(y1>0 && x1>0 ) ret += psum[y1-1][x1-1];
return ret;
}
int main()
{
int n;
vector< vector<int> > psum;
cin >> n;
int a;
psum.resize(n);
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
cin >> a;
if(i==0 && j==0) psum[i].push_back(a);
else if(i==0){
psum[i].push_back(a+psum[i][j-1]);
}
else if(j==0){
psum[i].push_back(a+psum[i-1][j]);
}
else
{
psum[i].push_back(a + psum[i-1][j] + psum[i][j-1] - psum[i-1][j-1]);
}
}
}
int x1,y1,x2,y2;
int m;
cin >> m;
for(int i=0;i<m;i++)
{
cin >> y1 >> x1 >> y2 >> x2;
cout << gridSum(psum,y1,x1,y2,x2) << endl;
}
return 0;
}
|
cs |
사업자 정보 표시
원당컴퓨터학원 | 기희경 | 인천 서구 당하동 1028-2 장원프라자 502호 | 사업자 등록번호 : 301-96-83080 | TEL : 032-565-5497 | Mail : icon001@naver.com | 통신판매신고번호 : 호 | 사이버몰의 이용약관 바로가기
'강의자료 > 알고리즘' 카테고리의 다른 글
| [알고리즘] Floyd-Warshall(플로이드워셜) 알고리즘 (14) | 2023.03.09 |
|---|---|
| [알고리즘] 크루스칼알고리즘 (12) | 2023.02.23 |
| [알고리즘] 조합탐색 (12) | 2023.02.01 |
| [알고리즘] 동적계획법(Dynamic) (12) | 2023.01.18 |
| [알고리즘] 분할정복 (12) | 2023.01.11 |