[알고리즘] 조합탐색

강의자료/알고리즘

[알고리즘] 조합탐색

원당컴1 2023. 2. 1. 10:15

조합탐색이란?

- 완전 탐색 알고리즘은 대개 답을 만드는 과정을 여러개의 선택으로 나눈 뒤 재귀 호출을 이용해 각각의 선택지를 채워가는 형태로 구현됨

- 기존 완전 탐색은 모든 답을 다 만들어 보면서 문제를 해결하므로 완전 탐색의 수행시간은 탐색 공간의 크기에 직접적으로 비례

- 이는 문제의 규모에 따라 기하급수적으로 크기가 증가.

- 조합탐색이란 완전 탐색을 포함해 유한한 크기의 탐색 공간을 뒤지면서 답을 찾아 내는 알고리즘

목표

- 기본적으로 모두 최적해가 될 가능성이 없는 답들을 탐색하는 것을 방지하여 만들어 봐야 하는 답의 수를 줄이는 것을 목표로 함

조합탐색 최적화 기법

- 가지치기 : 탐색 과정에서 최적해로 연결될 가능성이 없는 부분을 잘라낸다.

예) 외판원 문제에서 길이가 10인 경로를 이미 찾아 냈다고 하면 10보다 더 큰 값이 들어 오는 경우 탐색을 중단하는것.

- 탐색의 순서를 바꾸거나 탐색 시작전에 적당히 좋은 답을 우선 찾아 낸다.

조합탐색 기법들

외판원문제

여러 도시들이 주어져 있고, 모든 도시들에 대한 가중치가 주어졌을때, 단일 시작점부터 시작해서 모든 도시를 단 한번씩만 방문하여 다시 시작점으로 돌아오는데 드는 최단 거리를 구하는 문제(NP-하드 문제)

조합탐색의 뼈대 구현

/* TSP를 해결하는 완전 탐색의 구현(최적화가 되어 있지 않음)*/

const double INF = 1e200;
const int MAX = 30;
int n; //도시의 수
double dist[MAX][MAX]; //두 도시간의 거리를 저장하는 배열
//지금까지 찾은 최적해
double best;
//path:지금까지 만든 경로
//visited:각 도시의 방문 여부
//currentLength: 지금까지 만든 경로의 길이
//나머지 도시들을 모두 방문하는 경로들을 만들어 보고 가능하면 최적해를 갱신한다.
void search(vector& path, vector& visited, double currentLength) {
	int here = path.back();
	//기저 사례: 모든 도시를 다 방문했을 때는 0번 도시로 돌아가고 종료한다.
	if (path.size() == n) {
		best = min(best, currentLength + dist[here][0]);
		return;
	}
	//다음 방문할 도시를 전부 시도해 본다.
	for (int next = 0; next < n; ++next) {
		if (visited[next]) continue;
		path.push_back(next);
		visited[next] = true;
		//나머지 경로를 재귀 호출을 통해 완성한다.
		search(path, visited, currentLength + dist[here][next]);
		visited[next] = false;
		path.pop_back();
	}
}
double solve() {
	//best를 매우 큰 값으로 초기화
	best = INF;
	vector visited(n, false);
	vector path(1, 0);
	visited[0] = true;
	search(path, visited, 0);
	return best;
}

찾아야할 경로의 첫 도시는 항상 0으로 고정했기 때문에 search()가 만드는 경로의 수는 (n-1)!개

- 소형 데이터인 경우 빠르지만 대형 데이터의 경우 시간이 기하급수적으로 늘어남

최적해 보다 나빠지면 그만두기

if(best <=currentLength) return;

휴리스틱을 이용한 가지치기

: 휴리스틱이란 어림하여 값에 접근하는 방법

- 가지치기 중 특정 부분에서 최적해가 나올 수 없다는 것을 일찍 파악하는 것이 매우 중요

- 휴리스틱을 이용한 가지치기

. 남은 조각들을 푸는 최적해를 찾기는 오래 걸리더라도 이 값을 적당히 어림짐작하기는 훨씬 빠르게 할 수 있음

. 휴리스틱 반환 값이 항상 정확하지 않을 수 있음

(해결방법) 휴리스틱 반환값이 항상 남은 최단 경로의 길이보다 작거나 같게 함

휴리스틱 함수의 구현

solve()에서 각 도시마다 가장 가까운 도시까지의 거리를 미리 계산함.

/* 단순한 휴리스틱을 이용한 가지치기 구현*/

//각 도시에 인접한 간선 중 가장 짧은 것을 미리 찾아 둔다.
double minEdge[MAX];
//가장 단순한 형태의 휴리스틱
double simpleHeuristic(vector& visited) {
	double ret = minEdge[0]; // 마지막에 시작점으로 돌아갈 때 사용할 간선
	for (int i = 0; i < n; ++i)
		if (!visited[i])
			ret += minEdge[i];
	return ret;
}
void search(vector& path, vector& visited, double currentLength) {
	//단순한 휴리스틱을 이용한 가지치기
	if (best <= currentLength + simpleHeuristic(visited)) return;

	int here = path.back();
	//기저 사례: 모든 도시를 다 방문했을 때는 0번 도시로 돌아가고 종료한다.
	if (path.size() == n) {
		best = min(best, currentLength + dist[here][0]);
		return;
	}
	//다음 방문할 도시를 전부 시도해 본다.
	for (int next = 0; next < n; ++next) {
		if (visited[next]) continue;
		path.push_back(next);
		visited[next] = true;
		//나머지 경로를 재귀 호출을 통해 완성한다.
		search(path, visited, currentLength + dist[here][next]);
		visited[next] = false;
		path.pop_back();
	}
}

double solve() {
	//simpleHeuristic을 위한 초기화
	for (int i = 0; i < n; ++i) {
		minEdge[i] = INF;
		for (int j = 0; j < n; ++j)
			if (i != j) minEdge[i] = min(minEdge[i], dist[i][j]);
	}

	//best를 매우 큰 값으로 초기화
	best = INF;
	vector visited(n, false);
	vector path(1, 0);
	visited[0] = true;
	search(path, visited, 0);
	return best;
}

가까운 도시부터 방문하기

TSP에서 도시들이 몇 개씩 뭉쳐있는 경우 멀리 있는 도시보다 가까운 도시를 먼저 방문하는 경우가 유리한 경우가 많음
도시들을 미리 정렬해서 저장한 후 계산

/*가까운 정점부터 방문하는 최적화 구현*/
//각 도시마다 다른 도시들을 가가운 순서대로 정렬해 둔다.
vectornearest[MAX];
void search(vector& path, vector& visited, double currentLength) {
	//단순한 휴리스틱을 이용한 가지치기
	if (best <= currentLength + simpleHeuristic(visited)) return;

	int here = path.back();
	//기저 사례: 모든 도시를 다 방문했을 때는 0번 도시로 돌아가고 종료한다.
	if (path.size() == n) {
		best = min(best, currentLength + dist[here][0]);
		return;
	}
	//다음 방문할 도시를 전부 시도해 본다.
	for (int i = 0; i < nearest[here].size(); ++i) {
		int next = nearest[here][i];

		if (visited[next]) continue;
		path.push_back(next);
		visited[next] = true;
		//나머지 경로를 재귀 호출을 통해 완성한다.
		search(path, visited, currentLength + dist[here][next]);
		visited[next] = false;
		path.pop_back();
	}
}

double solve() {
	//nearest 최기화
	for (int i = 0; i < n; ++i) {
		vector> order;
		for (int j = 0; j < n; ++j) {
			if (i != j)
				order.push_back(make_pair(dist[i][j], j));
		}
		sort(order.begin(), order.end());
		nearest[i].clear();
		for (int j = 0; j < n - 1; ++j)
			nearest[i].push_back(order[j].second);
	}

	//best를 매우 큰 값으로 초기화
	best = INF;
	vector visited(n, false);
	vector path(1, 0);
	visited[0] = true;
	search(path, visited, 0);
	return best;
}

지나온 경로를 이용한 가지치기

이제까지 만든 경로가 최적의 경로가 아닌 경우 남은 조각들에서 아무리 선택을 잘해봐야 최적해를 찾지 못하고 계속 탐색을 할 이유가 없음.

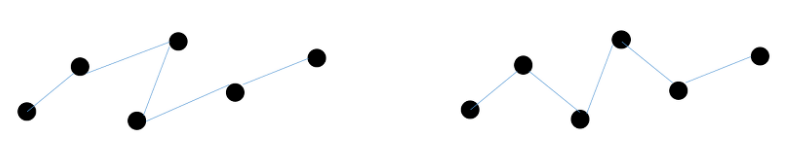
왼쪽에 있는 그림에서 3번째로 방문하는 도시와 4번째로 방문하는 도시의 순서를 바꾸면 오른쪽 그림처럼 된다.
오른쪽의 그림은 왼쪽의 그림보다 경로가 더 짧다.
따라서 탐색시 왼쪽 그림의 경로대로 따라가면 아무리 효율적으로 완성해 봐야 최적해가 될 수 없기 때문에 이 경우에는 탐색을 중단해도 된다.
TSP에서는 이런 원리를 구현하기 위해 인접한 둘의 순서를 바꾸어 본 뒤 경로가 더 짧아지면 탐색을 중단하는 가지치기를 구현하는 것이 가능
기존 구간(p,a,b,q, here) -> 변경 구간(p,b,a,q,here)

이 때 p-q 구간의 거리가 더 짧아진다면 이 경로에서 최적해를 찾을 가능성이 없으니 탐색 중단

/*지나온 경로를 이용하는 두 가지 가지치기 전략의 구현 */
//path의 마지막 네 개의 도시 중 가운데 있는 두 도시의 순서를 바꿧을 때
//경로가 더 짧아지는지 여부를 반환한다.
bool pathSwapPruning(const vector& path){
  if(path.size() < 4) return false;
  int p = path[path.size() -4];
  int a = path[path.size() -3];
  int b = path[path.size() -2];
  int q = path[path.size() -1];
  return dist[p][a] + dist[b][q] > dist[p][b] + dist[a][q];
}
//시작 도시와 현재 도시를 제외한 path의 부분 경로를
//뒤집어보고 더 짧아지는지 확인한다.
bool pathReversePruning(const vector& path){
  if(path.size() < 4) return false;
  int b = path[path.size() -2];
  int q = path[path.size() -1];
  for(int i = 0; i + 3 < path.size(); ++i){
    int p = path[i];
    int a = path[i+1];
    //[.., p, a, b, q]를 [p, b, a, q]로 바꾸어 본다.
    if(dist[p][a] + dist[b][q] > dist [q][b] + dist[a][q])
      return true;
  }
  return false;
}

pathSwapPruning()
search() 함수 처음에 pathSwapPruning()을 수행 후 참이 들어오면 탐색 종료(이 때 모든 도시가 아닌 현재 도시 이전의 두 도시만 체크)
한 도시 뒤에 경로가 추가될 때마다 pathSwapPruning이 수행

pathReversePruning()
전체 경로의 일부분을 통째로 뒤집는 것으로 일반화 가능
(p,a,b,c,d,e,q,here) -> 길이가 5인 부분 경로(a,b,c,d,e)를 뒤집기 -> (p,e,d,c,b,a,q,here)
경로 자체의 길이는 똑같기 때문에 달라지는 것은 p와 q에 인접한 도시일 뿐
q=here인 경우 현재 이전 도시에서 끝나는 경로들을 뒤집는 경우만을 고려

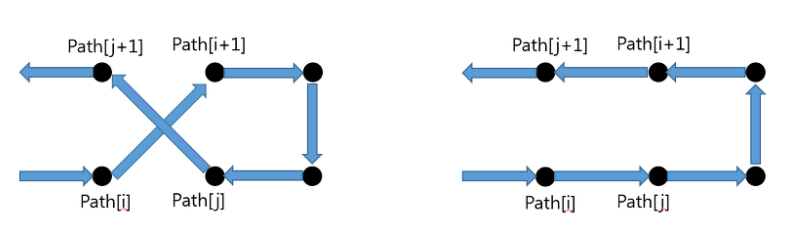
왼쪽 그림은 path가 서로 교차하는 것을 보여줌
오른쪽 그림은 교차된 선을 일직선으로 바꾸엇을 때를 보여줌
교차했을 때보다 더 짧아짐.
pathReversePrunning은 모든 길이의 부분 경로를 뒤집어보기 때문에 이전 방법보다 더 많은 경우를 가지치기할 수 있음

저작자표시

사업자 정보 표시

'강의자료 > 알고리즘' 카테고리의 다른 글

[알고리즘] 크루스칼알고리즘 (12)	2023.02.23
[알고리즘] 부분합 (8)	2023.02.08
[알고리즘] 동적계획법(Dynamic) (12)	2023.01.18
[알고리즘] 분할정복 (12)	2023.01.11
[자료구조] Suffix Array(접미사 배열) (11)	2023.01.04

현재글[알고리즘] 조합탐색

검단신도시 코딩/컴퓨터기초/컴퓨터자격증/C++/JAVA/Python/정보올림피아드 전문 학원

원당컴퓨터학원