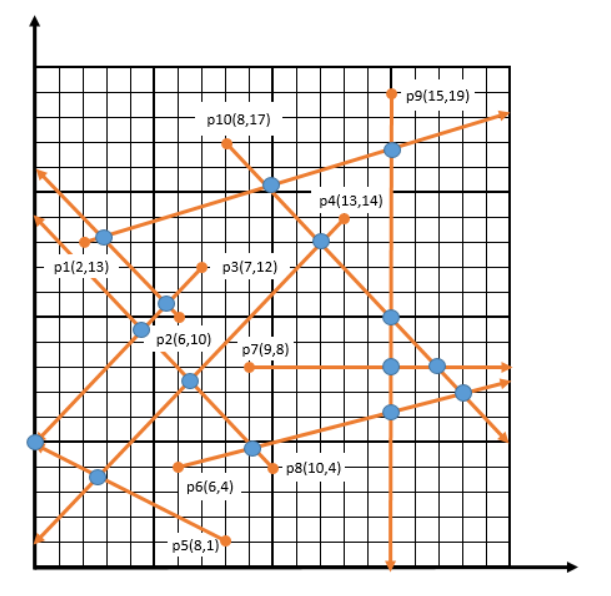
이산 수학을 공부하다 보면 행렬에 관한 문제를 풀게 되는데요. 행렬을 배우다 보면 행렬식을 배우게 됩니다. 영어로는 determinant 라고 하면서 계산 하는 방법은 다음과 같습니다. A 행렬이 다음과 같이 구성 되어 있을때 행렬식 det(A) = a11 * a22 - a12 * a21 과 같이 계산이 됩니다. 그렇다면 이러한 행렬식이 의미하는 것은 무엇일까요? 알고리즘에서 기하문제가 종종 나오는데... 기하 문제에서 사용하는 사각형의 부피를 구할때 이 행렬식을 이용하기도 합니다. 오늘은 이 두개의 벡터가 이루고 있는 평행사변형의 넓이에 대해 알아 볼까 합니다. 위와 같은 벡터가 두개가 있는 경우 행렬식은 이 벡터를 선형 변환 후 두 기저벡터가 이루고 있는 평행사변형의 넓이를 의미합니다. 이것을 벡터의..