머신러닝 목차 - https://wondangcom.tistory.com/2769
머신러닝 목차
머신러닝1. 머신러닝 소개1.1 인공지능이란(혼공머신) - 4차산업 혁명 시대에 꼭 필요한 인공지능에 대해 알아 보자.링크 : https://wondangcom.tistory.com/2771(2024.3.7) 1.1 인공지능이란목표 4차 산업 혁
wondangcom.tistory.com
딥러닝
우리는 사람처럼 생각하는 기계를 만들고 싶었다.
여러가지 알고리즘 중 하나가 사람의 뇌의 형태를 본 따서 만드는 것이었다.

뇌의 신경망을 살펴보니 복잡하게 되어 있는 줄 알았는데 각각의 뉴런은 여러 개의 입력에 대해 하나의 출력을 다른 뉴런에게 전달하는 구조로 되어 있는 것을 확인하였다.

입력 되는 신호는 길이에 따라 달라지는 것을 확인 하였고 이것을 XW+b 와 같이 각각의 서로 다른 값을 가져간다고 하면 인공신경망(Ann)을 구현 할 수 있게 된다.
(Neurones -> nodes, Synapses -> weights)
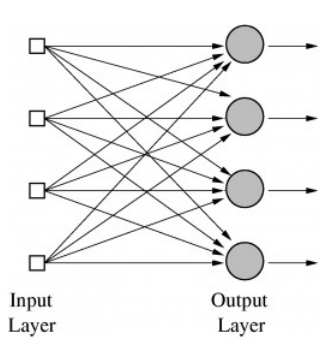
4개의 입력이 4개의 뉴런에 전달 되는 모습
OutputLayer의 각각의 뉴런은 서로 다른 Weight 와 Bias를 가지고 있고 다른 활성화 함수(Activation)에 의해 같은 입력 값이라도 출력값은 서로 다르다.
가령 Output Layer가 각각마다 사과를 판단하는 뉴런,바나나를 판단하는 뉴런,귤을 판단하는 뉴런,당근을 판단하는 뉴런이라고 했을 때 같은 이미지 데이터 가령 사과라는 이미지가 들어 왔다면 사과를 판단하는 뉴런이 활성화 되어 사과라는 것을 판단하게 된다.
초창기의 인공지능

초기에는 and와 or 문제를 풀 수 있다면 선형에 관한 문제를 해결 할 수 있다고 생각했다.
하지만 XOR 문제가 대두되면서 이 문제를 선형으로 해결 할 수 있는 방법을 찾을 수 없었다.

단순히 논리 회로에서 and 게이트와 or 게이트를 사용하여 xor 게이트를 만드는 것은 간단하지만 이것을 인공신경망을 이용하여 해결하는 방법은 찾을 수가 없었다.
퍼셉트론(Perceptrons)
1943년에 맥컬럭 월터 피츠는 ANN의 가능성을 처음으로 주장하였다.
1957년 미국의 신경생물학자인 프랑크 로젠블랫은 이 개념을 실증하는데 성공했고 퍼셉트론이라고 불렀다. 하지만 위와 같이 XOR 문제를 해결하지 못하면서 묻혔다가~
1969년 Marvie Minske 교수는 한개의 Layer 가 아닌 여러 개의 Layer를 가지고 XOR 문제를 해결 할 수 있다고 발표 하였다.(다층 퍼셉트론)

하지만 Minske 교수는 이것을 구현할 수 있는 방법을 찾지는 못했다.
1986년 Hinton 교수는 Backpropagation(역전파) 알고리즘으로 다층 퍼셉트론을 학습시키는데 성공하였다.

이러한 다층 퍼셉트론은 1989년 얀 레쿤과 요슈아 벤지오가 CNN 을 완성한다.
딥러닝으로 XOR 문제 해결하기 실습

XOR의 속성은 위와 같이 x1와 x2가 같은 경우 0, 서로 다른 경우 1이 나오는 것이다.
이것을 하나의 선으로는 구분 할 수가 없고 다음과 같이 세 개의 네트웍을 가지고 만들 수 있다.

세개의 네트웍에 첫번째 네트웍 Weight=[5,5],bias=-8,두번째 네트웍은 Weight=[-7,-7],bias=3,세번째 네트웍은 Weight=[-11,-11],bias=6 이라는 값을 임의로 지정한 다음
첫번째 네트웍과 두번째 네트웍에서 나온 값을 세번째 네트웍의 입력 데이터로 만들어서 세번째 네트웍의 출력값을 살펴 보자. 시그모이드 활성화 함수를 사용하기 때문에 출력값이 0보다 크면 출력(1),아니면 (0)으로 표를 생성해 보자.
import matplotlib.pyplot as plt
x_data = [[0, 0],
[0, 1],
[1, 0],
[1, 1]]
plt.scatter(x_data[0][0],x_data[0][1], c='red' , marker='^')
plt.scatter(x_data[3][0],x_data[3][1], c='red' , marker='^')
plt.scatter(x_data[1][0],x_data[1][1], c='blue' , marker='^')
plt.scatter(x_data[2][0],x_data[2][1], c='blue' , marker='^')
plt.xlabel("x1")
plt.ylabel("x2")
plt.show()
위와 같이 x데이터를 생성하여 분류가 되는지를 살펴 본다.
w1 = [5,5]
b1 = -8
w2 = [-7,-7]
b2 = 3
w3 = [-11,-11]
b3 = 6
print('x1','x2','y1','y2','y3')
for i in range(4):
x = x_data[i]
#첫번째 네트웍을 통과한 값을 a1의 출력값으로 만든다.
z1 = x[0]*w1[0] + x[1]*w1[1] + b1
if z1 <= 0:
a1 = 0
else:
a1 = 1
#두번째 네트웍을 통과한 값을 a1의 출력값으로 만든다.
z2 = x[0]*w2[0] + x[1]*w2[1] + b2
if z2 <= 0:
a2 = 0
else:
a2 = 1
#첫번째 네트웍과 두번째 네트웍을 통과한 출력을 입력으로 받아 세번째 네트웍의 출력값으로 만든다.
z3 = a1*w3[0] + a2*w3[1] + b3
if z3 <= 0:
a3 = 0
else:
a3 = 1
print(x[0],x[1],a1,a2,a3)
x1,x2 가 서로 다를때만 y3이 1이 되는 것을 확인해 볼 수 있다.
이것은 적당한 Weight와 bias를 찾아 준다면 xor를 해결 할 수 있다는 것을 보여 준다.
위의 그림은 다음과 같이 행렬을 이용한 네트웍으로 표현 할 수 있다.

처음 나오는 유닛 두개를 하나의 유닛으로 뭉쳐서 2차원 벡터로 표현 할 수 있게 된다.
이것을 수식으로 표현하면 다음과 같이 표현 할 수 있다.
$$ K(X) = sigmoid(XW_1+_1) $$
$$ \overline{y} = sigmoid(K(X)W_2+b_2) $$
이것을 텐서플로우로 구현하면 다음과 같이 될 것이다.
import tensorflow as tf
x_data_tensor = tf.constant(x_data, dtype=tf.float32)
W1 = tf.constant([[5,-7],[5,-7]], dtype=tf.float32)
B1 = tf.constant([-8,3], dtype=tf.float32)
W2 = tf.constant([[-11],[-11]], dtype=tf.float32)
b2 = 6
K = tf.sigmoid(tf.matmul(x_data_tensor,W1)+B1)
hypothesis = tf.sigmoid(tf.matmul(K,W2)+b2)
print(hypothesis)
시그모이드 함수값이므로 0.5 이하는 0,초과는 1로 판단하면 0,1,1,0 이 나오는 것을 확인 할 수 있다.
그렇다면 이러한 Weight과 Bias를 어떻게 학습 시킬 수 있을까?
Weight과 Bias의 학습 원리
우리가 잘 알고 있는 Gradiant Decent 알고리즘으로 이 Weight와 Bias를 찾아 낼 수 있다.
y^을 가지고 cost 비용을 구해서 그 비용이 점점 줄어드는 방향으로 Weight와 Bias를 찾아내는 원리이다.
1986년 힌톤 교수에 의해서 역전파 알고리즘이 구현 되었는데 이 것은 예측한 값과 결과값의 오류를 뒤에서 부터 앞쪽으로 되돌려 주면서 Weigt와 Bias 값을 적용하겠다는 것이다.
실제로 동작하는 원리를 살펴 보자.

f 라는 함수는 WX + b 형태로 되어 있는데 WX를 g로 바꿔 보면 f = g+ b와 같은 형태로 표현 할 수 있다.
이 때 W 가결과값에 미치는 영향은 결과값을 W로 미분한 값에 해당한다.

여기서 w= -2,x=5,b=3 이라고 가정할 때
g = -2*5 = -10 이 되고 f= -7 이 된다.
f=wx+b,g=wx,f=g+b 에서 미분하는 과정을 살펴 보면
g = wx 에서 g를 w로 미분하면 x(x=5) 가 된다. g를 x로 미분하면 w(w=-2) 가 된다.
다음으로 f = g + b에서 f를 g로 미분하면 1,f를 b로 미분하면 1 이 된다.
이것을 그래프로 살펴 보면 다음과 같다.

다음 단계로 f를 w로 미분하는 것과 f를 x로 미분하는 것을 살펴 보면 된다.
$$ \frac{\partial f}{\partial w} = \frac{\partial f}{\partial g} \frac{\partial g}{\partial w} $$
f를 w로 미분하면 위와 같이 f를 g로 미분한 값의 곱과 g를 w로 미분한 값의 곱으로 표현 할 수 있다.
여기서 f를 g로 미분한 값은 1, g를 w로 미분한 값은 x 이므로 1*5=5 가 된다.
다음으로 f를 x로 미분한 값은 다음과 같이 구할 수 있다.
$$ \frac{\partial f}{\partial x} = \frac{\partial f}{\partial g} \frac{\partial g}{\partial x} $$
여기서 f를 g로 미분한 값은 1,g를 x로 미분한 값은 w이므로 -2 가 된다.
그림으로 살펴 보면 다음과 같이 되는 것을 확인 할 수 있다.

여기서 w의 미분값이 5라면 w를 1 만큼 바꾸면 출력의 결과값은 5배 만큼 바뀐다는 의미이다.
이러한 의미를 이용해서 마지막 결과값을 원하는 값으로 나올 수 있게 조정하는 것이 역전파이다.
텐서플로우에서 코드 실습
y_data = [[0],
[1],
[1],
[0]]
#데이터 전처리
dataset = tf.data.Dataset.from_tensor_slices((x_data, y_data)).batch(len(x_data))
def preprocess_data(features, labels):
features = tf.cast(features, tf.float32)
labels = tf.cast(labels, tf.float32)
return features, labelsweigt와 bias를 훈련하기 위해 라벨을 생성 후 텐서플로우에서 입력 가능한 데이터로 전처리 한다.
batch 크기는 x_data 전체로 잡았고 preprocess_data 에서 features 와 labels의 Data 연산을 위해 int -> float Type으로 맞춰 준다.
W1 = tf.Variable(tf.random.normal((2, 1)), name='weight1')
b1 = tf.Variable(tf.random.normal((1,)), name='bias1')
W2 = tf.Variable(tf.random.normal((2, 1)), name='weight2')
b2 = tf.Variable(tf.random.normal((1,)), name='bias2')
W3 = tf.Variable(tf.random.normal((2, 1)), name='weight3')
b3 = tf.Variable(tf.random.normal((1,)), name='bias3')W1,W2,W3 을 2*1 형태의 랜덤 값으로 생성하였다.
def neural_net(features):
layer1 = tf.sigmoid(tf.matmul(features, W1) + b1)
layer2 = tf.sigmoid(tf.matmul(features, W2) + b2)
layer3 = tf.concat([layer1, layer2],-1)
layer3 = tf.reshape(layer3, shape = [-1,2])
hypothesis = tf.sigmoid(tf.matmul(layer3, W3) + b3)
return hypothesislayer1 과 layer2의 출력을 layer3의 입력 데이터로 만들어서 예측하는 모델을 만들었다.
def loss_fn(hypothesis, labels):
cost = -tf.reduce_mean(labels * tf.math.log(hypothesis) + (1 - labels) * tf.math.log(1 - hypothesis))
return cost
optimizer = tf.keras.optimizers.SGD(learning_rate=0.01)비용함수를 선언하였다.
비용함수는 다음과 같은 수식으로 생성된다.

def accuracy_fn(hypothesis, labels):
predicted = tf.cast(hypothesis > 0.5, dtype=tf.float32)
accuracy = tf.reduce_mean(tf.cast(tf.equal(predicted, labels), dtype=tf.float32))
return accuracy추론한 값을 0.5 초과이면 1, 아니면 0으로 만든 후 실제 데이터와 비교하여 점수를 반환하는 함수를 만들었다.
def grad(hypothesis, features, labels):
with tf.GradientTape() as tape:
loss_value = loss_fn(neural_net(features),labels)
return tape.gradient(loss_value, [W1, W2, W3, b1, b2, b3])features 를 neural_net을 통해 모델을 통해 예측한 후에 loss_fn을 통해 손실값을 계산 하였고 tape.gradient 를 통해 경사값을 계산하는 함수를 만들었다.
EPOCHS = 50000
for step in range(EPOCHS):
for features, labels in dataset:
features, labels = preprocess_data(features, labels)
grads = grad(neural_net(features), features, labels)
optimizer.apply_gradients(grads_and_vars=zip(grads,[W1, W2, W3, b1, b2, b3]))
if step % 5000 == 0:
print("Iter: {}, Loss: {:.4f}".format(step, loss_fn(neural_net(features),labels)))
x_data, y_data = preprocess_data(x_data, y_data)
test_acc = accuracy_fn(neural_net(x_data),y_data)
print("Testset Accuracy: {:.4f}".format(test_acc))
50000번을 반복하면서 훈련후 마지막에 훈련된 Weight와 Bias를 가지고 예측을 했을때 100 프로로 정확히 예측하는 것을 알 수 있다.
참고)
텐서플로우로 다지는 기초
'강의자료 > 머신러닝' 카테고리의 다른 글
| 7.2 Convolution Layer 실습 (3) | 2024.08.23 |
|---|---|
| 7.1 CNN이란? (5) | 2024.08.16 |
| keras 2.x -> keras 3.x 으로 변경 되면서 수정 되는 사항 (3) | 2024.08.08 |
| 5.2 차원축소 (3) | 2024.08.01 |
| 5.1 군집분석 (5) | 2024.07.26 |